Produktionsteori strävar efter att förklara hur ett företag bör fatta beslut om hur mycket av en vara de ska producera (dess "output") och hur stor mängd av olika insatsvaror (dess "input") som ska användas i produktionen. En viktig del av detta är att beräkna kostnader och intäkter för olika kvantiteter, eftersom företagen måste ta hänsyn till priserna som de kan köpa insatsvaror och sälja slutprodukten till. Målet med produktionen är vinstmaximering. Man brukar för enkelhetens skull oftast bara definiera två övergripande typer av insatsvaror (produktionsfaktorer):
Priserna på dessa insatsvaror utgörs av:
Produktion Lagen om den marginellt avtagande avkastningen (Law of diminishing marginal returns) Om en insatsvara ökas och övriga insatsvaror hålls konstanta så kommer förr eller senare ökningstakten i den totala produktionen att börja avta (se andra diagrammet nedan). Exempel: Om vi fortsätter hälla säd på en redan sådd mark så kommer växandet öka i en allt mer avtagande takt. Marginalprodukten av arbetskraft (MPL, Marginal product of labor) Produktionsökningen av att anställa ytterligare en person. Det vill säga, förändringen i den producerade kvantiteten när arbetskraften ökar eller minskar med en enhet. Exempel: L ökar från 0 till 1. Delta L = 1 - 0 Q ökar från 0 till 4. Delta Q = 4 - 0 MPL = (4-0) / (1-0) = 4 Isokvant (Isoquant) Från http://en.wikipedia.org/wiki/Isoquant (även efterföljande diagram) En kurva som visar alla kombinationer av två insatsfaktorer (oftast kapital och arbetskraft) som ger upphov till en viss producerad kvantitet av varan (Q). Exempelvis kan man beskriva hur ett förhållande mellan arbetare och spadar skulle se ut för att producera en viss mängd av en vara så effektivt som möjligt. Isokvanten kan vara mer eller mindre linjär respektive L-formad:
Kostnader Ett företags kostnader utgörs av mängden insatsvaror som används i produktionen och insatsvarornas pris: Totala kostnader (TC, Total cost) = w * L + r * KTC kan delas upp i två delar, där TC = VC + FC:
Man brukar skilja mellan två tidsrymder.
Vi kan beräkna en mängd ytterligare kostnadsvariabler som varierar beroende på producerad kvantitet:
När marginalkostnaden (MC) överstiger de variabla eller totala genomsnittskostnaderna (ATC eller AVC) så börjar dessa stiga. MC skär därför AVC och ATC vid deras minimum precis när deras lutning är flak. Eftersom fasta kostnader (FC) är konstanta, oberoende av producerad kvantitet, så minskar de fasta genomsnittskostnaderna (AFC) ständigt i takt med att kvantiteten ökar. AFC är därför en ständigt avtagande kurva. Eftersom ATC = AFC + AVC så ser vi att ATC och AVC närmar sig allt mer när kvantiteten ökar eftersom AFC minskar. Isokostlinje (isocost line) Visar kombinationer av två insatsvaror (oftast arbetskraft och kapital) som ger samma totala kostnader (TC). Eftersom båda insatsvarorna måste vara rörliga så brukar isokostlinjen enbart gälla på lång sikt. Matematisk definition: C = wL + rK Exempel: C = 7 (de totala kostnaderna är 7) 7 = wL + rK
Kostnadsminimering För att producera en viss kvantitet till lägsta kostnad krävs den mängd K och L som ges av tangeringspunkten mellan isokvanten och isokostlinjen. Vid kostnadsminimering gäller att: MPL / MPK = w/r Eftersom w/r är konstanta faktorer (företagen har inte tillräckligt mycket makt över ränte- och lönemarknaden) så måste förändringar ske i MPL / MPK
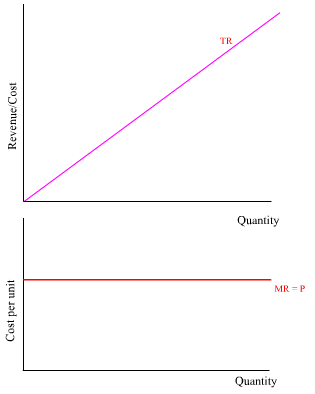
Intäkter Variationer: Konkurrensutsatt marknad P* = Marknadspriset som företaget måste rätta sig efter (företaget kan inte förändra priset) q = Ett enskilt företags kvantitet (en liten del av marknadens kvantitet) Eftersom priset är låst till marknadspriset så ger varje ytterligare såld enhet en ökning identisk med priset, dvs MR = priset. Därför ökar de totala intäkterna konstant ju mer man säljer. Monopolistisk marknad P = Marknadspriset som företaget sätter (eftersom den är ensam aktör på marknaden) Q = Marknadens/Företagets producerade kvantitet (identiska eftersom företaget är ensam aktör på marknaden) Eftersom priset per enhet sätts av företaget beroende på antalet producerade enheter så får TR formen av ett upp och nedvänt "u", och når ett max när den producerade kvantiteten för det efterfrågade priset ger som störst intäkter. Detta inträffar alltid vid hälften av efterfrågekurvan (vid enhetselasticitet) och gör att MR-kurvan sluttar tills den når 0 vid just denna punkt.
Vinstmaximering Det finns olika sätt att räkna ut den vinstmaximerande kvantiteten (och priset):
Exempel: Fråga Säg att vi känner till TR och TC för ett företag: TR = 120Q - 0.5Q² TC = 420 + 60Q + Q² Hur tar vi reda på vinstmaximerande kvantitet och pris? Svar ∏ = TR - TC ∏ = (120Q - 0.5Q²) - (420 + 60Q + Q²) ∏= -420 + 60Q - 1.5Q² ∏’ = 60 - 3Q ∏’ = 0 60 - 3Q = 0 60 = 3Q Q = 20 The profit maximizing quantity is 20. To find the profit maximizing price you need the price equation: TR = PxQ P = TR/Q Vi kan nu placera in värdet av TR i prisekvationen: TR = 120Q - 0.5Q² P = 120Q - 0.5Q²/Q P = 120 - 0.5Q P = 120 - 0.5(20) P = 120 - 10 P = 110 The results can be checked by using the standard rule for maximizing profits - equating marginal revenue (MR) and marginal costs (MC). TR = 120Q - 0.5Q² MR = 120 - Q TC = 420 +60Q + Q² MC = 60 + 2Q MR = MC 120 - Q = 60 + 2Q 60 = 3Q Q = 20 |
Mikroekonomi >