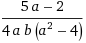Ekvationssystem:

5x + 2y = 3

2x + 3y = -1

Svar:

Löser ut y i första ekvationen:

5x + 2y = 3

2y = 3 - 5x

y = 1,5 - 2,5x

Kan nu stoppa in i andra ekvationen

2x + 3y = -1

2x + 3(1,5 - 2,5x) = -1

2x + 4,5 - 7,5x = -1

-5,5x + 4,5 = -1

Lägger till 5.5x, drar av 1:

5,5 = 5,5x

x = 1

Stoppa in x i första ekvationen:

5x + 2y = 3

5 * 1 + 2y = 3

2y = -2

y = -1

f(t) = A * e^rt 

g(t) = B * e^st 

När är f(t) = g(t)?

r får inte vara lika med s

Skulle kunna vara två länders BNP. Länderna börjar på A resp B.växer med r resp s. Hur många år skulle behöva gå innan länderna är lika stora?

Att r inte får vara samma som s innebär att länderna måste växa olika fort. Om de vore samma skulle de aldrig mötas.

A/B/s/r kan vara vad som helst i varje led, så vi vill snarare ta reda på t.

A * e^rt = B * e^st 

ln(A * e^rt) = ln(B * e^st) 

ln A + rt = ln B + st 

rt - st = ln B - ln A

(r - s)t = ln B - ln A

t = (ln B - ln A) / r - s

Lös ut x:

1 / ax + 1 / bx = 2

Multiplicera med ax * bx för att blir av med nämnarna (måste inte skaffa gemensamma nämnare):

1 / ax + 1 / bx = 2

axbx / ax + axbx/bx = 2axbx

bx + ax = 2abx² 

Dela med x:

b+a = 2abx

x = (a+b)/2ab

Alternativ lösning:

1 / ax + 1 / bx = 2

Multiplicera med x i alla leden:

1x / ax + 1x / bx = 2x

Ger oss:

1 / a + 1 / b = 2x

x = 1/2 (1/a + 1/b)

Summera från m = 0 till m = 5(?)

Svar:

Vi vet att den undre delen måste vara 0 för att resultatet ska bli det, kan därför ta bort den:

x * ln (x+3) = 0

Vi vet även att x eller ln (x+3) måste vara 0. Så vi ser att det finns två lösningar:

x = 0 eller ln (x+3) = 0

Om vi fortsätter på lösning två:

ln (x+3) = 0

Vi höjer upp e till båda leden:

e^{ln (x+3)} = e⁰ 

ln och e försvinner:

x + 3 = 1

x = -2

Botswanas befolkning var 1.22 miljoner och växer med hastigheten 3.4% varje år. Hur lång tid tar det för det hela att dubblas?

P = Befolkning

t = Antal år

P(t) = 1,22 * 1,034^t 

När är P(t) = 2,44 (befolkningen dubblad)?

Ekvation:

1,22 * 1,034^t = 2,44

1,034^t = 2

t * ln 1,034 = ln 2

t = ln 2 / ln 1,034 (knappa in på miniräknare)

2^x - 2^x-1 = 4

Funkar inte med ln eftersom det inte förenklar.

Lättare att faktorisera, dvs bryta ut:

2^x-1(2-1) = 4

Eftersom 2-1 = 1 så försvinner parentesen.

2^x-1 = 4

Vi vet att 2 upphöjt i 2 är 4, därför kan vi helt enkelt svara att:

2² = 4

Om det rört sig om variabler så hade vi behövt logratimera på båda sidor istället.

I Tanzania 15-årsplan där man vill dubblera realinkomst per capita. Vilken årlig tillväxttakt måste inkomsten?

(1 + r)¹⁵ = 2

Vi kan ta 15-roten ur båda leden. Kan skrivas som upphöjt i 1/15

[(1 + r)¹⁵]^1/15 = 2^1/15

1+r = 2^1/15

1+r = 1,0473

r = 0,0473 = 4,73%

d)

Vi vill slå samman nämnarna, och måste därför hitta en minsta gemensamma nämnare.

(ax + b) / (cx + d) = A

ax + b = A(cx+d)

ax + b = Acx + Ad

ax - Acx = Ad - b

x(a - Ac) = Ad - b

x = (Ad-b) / (a - Ac)

1000 kr på banken med 5% årlig ränta. Hur mycket har beloppet vuxit efter:

a) 10 år

Vi har två formler för slutvärde (future value):

Periodsvis kapitalisering: S = P(1+r)^t 

Kontinuerlig kapitalisering: S = P * e^rt 

a)

Årlig kapitalisering

1000 * 1,05¹⁰ = 1628,89

Månatlig kapitalisering (vi tar reda på ökningen varje månad

1000 * (1+0,05/12)¹²⁰ = 1647,01

Kontinuerlig kapitalisering (vi använder den andra formeln för slutvärde)

1000 * e^0,05*10 = 1648,72

Extra uppgift:

Välj mellan:

1) 5000 kr om tre år

2) 4000 kr nu

Väljer troligtvis 4000 kr nu. Pengar är mer värda idag än i framtiden. Frågan är vart gränsen går.

30 kr nu eller 5000 kr om tre år så väljer vi givetvis 5000 kr (om vi inte håller på att svälta).

Svårare vid t.ex. 2000 kr. Vi måste beakta vad som händer om vi sätter in pengarna på banken idag, vilket är beroende av räntan (r). Om en fast ränta garanterar att 2000 kr är värda mer än 5000 kr om tre år så är det givet att vi tar pengarna idag. Detta gör vi med hjälp av nuvärde.

Slutvärde:

Kan skrivas om till nuvärde:

Nuvärde:

Exempel:

5000 kr om 3 år:

Bankränta/Diskonteringsränta: 4%

Nuvärde = 5000 * 1,04^-3 

Nuvärde = 4444,98

Om vi får 4444,98 idag så är det lika mycket som att få 5000 kr om tre år.

Om vi om 10 år får 350 000. Vad får vi idag? Diskoteringsränta = 8%.

i) Årligen

ii) Kontinuerlig

i) Nuvärde = 350 000 * 1,08^-10 = 162 118

ii) Nuvärde = 350 000 * e^{-0,08 * 10} = 157 265

Behöver vi ta hänsyn till inflation om vi ska välja mellan pengar idag och i framtiden? Inte om vi talar om att ändå sätta in pengarna på banken. Inflationen har samma effekt på slutvärdet i bägge fallen.