Tentan: 60 poäng, 30 för godkänt Mikroteori i praktiken
Beslutsfattande
Prisbildningen viktig i alla delar Utbud och efterfråganSe även Utbud och efterfrågan Efterfrågan, utbudet, jämvikt där utbud = efterfrågan EfterfråganEfterfrågad kvantitet (Qd) är en funktion (D) av priset på varan (P), men även priset på substitut (Ps) och komplement (Pc). Den påverkas även av inkomsten (Y), för ju större inkomst man har, desto mer vill man konsumera. Qd = D(P, Ps, Pc, Y) Om priset blir dyrare vill man konsumera mindre av varan (negativt samband) Om ett substitut blir dyrare vill man konsumera mer (positivt samband) Om ett komplement blir dyrare vill man konsumera mindre (negativt samband) Om inkomsten blir högre vill man konsumera mer av varan En klassisk efterfrågekurva: Ps, Pc och Y är givet. Ändras P förflyttas vi utefter kurvan, men ändras någon av de andra så kommer kurvan att skiftas. Om t.ex. inkomsten (Y) ökar, så kommer vi att efterfråga mer av varan på alla prisnivåer, och kurvan förskjuts åt höger. Samma sak om en substitutvara blir dyrare. Medan om en komplementvara blir dyrar så förskjuts kurvan åt vänster. MarknadsefterfråganSummera efterfrågan på en marknad. Individuella efterfrågefunktioner (Q1, Q2 osv): Q1 = D1(P) Q2 = D2(P) Marknadsefterfrågan (Qtot): Qtot = Q1 + Q2 Exempel: UtbudUtbud (Qs) är en funktion (S) av priset på varan (P), men även priset på insatsvaror (a) Qs = S(P, a) Om varan är dyrare så kan det produceras mer, och utbudet blir större. Om insatsvarorna blir dyrare så produceras mindre, och utbudet blir mindre. a är givet. Ändras P så förflyttar vi oss utefter kurvan. Ändras a förskjuts hela kurvan. MarknadsutbudSamma som efterfrågan: Qtot = Q1 + Q2 Lägger samman alla företags utbudsfunktioner. MarknadsjämviktExempel: Qd = 80 - 10P Qs = 20P - 10 Reservationspris - Priset när Qs = 0, dvs fasta kostnader som inte är löpande kostnader Jämvikt: Qd = Qs 80 - 10P = 20P - 10 90 = 30P P* = 3 Q* = 50 Jämviktspriset kan ändras av andra faktorer än P: Om t.ex. inkomsten (Y) ökar så ökas jämvikten eftersom efterfrågan skiftar åt höger. Kanske från Qd = 80 - 10P till Qd = 90 - 10P Marginell förändringTittar återigen på de generella funktionerna, men förenklar efterfrågefunktionen genom att bara göra den till en funktion av priset. Qd = D(P) Qs = S(P, a) Jämvikt: Qd = Qs D(P) = S(P, a) Vad händer med jämvikten om a ändras? Om insatsvarorna ökar så vet vi att det produceras mindre, så utbudskurvan skiftar åt vänster. Vi får en minskning av jämviktskvantiteten och en ökning av jämviktspriset. Priset blir i sig en funktion av a. Kan därför skriva om jämvikten: D(P(a)) = S(P(a), a) Vad händer om a ändras marginellt? Kan derivera med avseende på a. Derviera först efterfrågan med avseende på priset (dD/dP), sen priset med avseende på insatsvarorna (dP/da). Osv. Partialderivatan (omvänt 6) dD/dP * dP/da = 6S/6P * dP/da + 6S/6a Tre effekter: När P ändras rör vi oss utefter D, som vi ser på: dD/dP * dP/da När P ändras så ändras S, vilket vi ser på: 6S/6P * dP/da Men vi har även en direkteffekt av insatsfaktorerna: 6S/6a Vad händer med P: dP/da? Vi kan lösa ut P: Flyttar över termer från högerledet: dP/da (dD/dP - 6S/6P) = 6S/6a Dela båda leden med (dD/dP - 6S/6P dP/da = 6S/6a / (dD/dP - 6S/6P) Vi har en negativ täljare genom en negativ nämnare. Vi får därför att resultatet måste bli större än 0. Vad händer med Q? Qd = D(P(a)) Vi måste derivera Q med avseende på a. dQd/da = dD/dP * dP/da Resultatet måste vara mindre än 0? Inte självklart att vi kan utläsa samma resultat från utbudssidan. Qs = S(P(a), a) dQs/da = 6S/6P * dP/da + 6S/6a 6S/6P: Positiv (indirekt effekt) dP/da: Positiv (indirekt effekt) 6S/6a: Negativ (direkt effekt, går åt andra hållet) Resultatet går inte att urskilja om det är större eller mindre än 0. Vid en utbudschock så bestäms ändringen av jämviktskvantiteten (Q*) av efterfrågan. Vid en efterfrågechock så bestäms ändringen av Q* av utbudet. Om det blir dyrare att producera så kommer den efterfrågade kvantiteten att minska. ElasticiteterSe även ElasticitetElasticitet = % förändring i x / % förändring i y = (Δx/x) / (Δy/y) = dx/dy * y/x Efterfrågans priselasticitetVad händer med den efterfrågande kvantiteten (Qd) om priset ökar med 1%?Efterfrågefunktion: Q = D(P) Elasticitet (ε) ε = % förändring i Qd / % förändring i P = (ΔQ/Q) / (ΔP/P) = dQ/dP * P/Q Både pris och kvantitet måste vara positiva tal. Vi brukar utvärdera elasticiteter just i jämviktspunkter, eftersom elasticiteten ändras utefter efterfrågekurvan. Man kan inte säga att man har samma priselasticitet överallt, för även en helt linjär efterfrågafunktion har olika priselasticitet vid olika delar: Elastisk: ε = -1 till -∞ Enhetselastisk: ε = -1 Fullkomligt oelastisk: ε = -1 till 0 Om vi utgår ifrån att vi har två konstanter, a och b. Qd = a - bP dQ/dP = -b ε = dQ/dP * P/Q ε = -b * P/Q -bp = Q-a ε = Q-a / Q ε = 1 - a/Q ε är en funktion av Q! Andra efterfrågeelasticiteterOm vi utgår ifrån den fullkomliga efterfrågefunktionen:Q = D(P, Ps, Pc, Y) Vi kan räkna ut efterfrågans priselasticitet som vi gjorde innan. Vi kan även räkna ut efterfrågans inkomstelasticitet: εd = % förändring i Q / % förändring i Y = 6Q/6Y * Y/Q Denna är större än 0 för normala varor Vi kan även räkna ut korspriselasticitet, dvs hur en varas pris påverkar en annan varas efterfråga. T.ex. två varor i och j: εij = % förändring i Qi / % förändring i Pj = 6Qi/6Pj * Pj/Qi Vi har en positiv korspriselasticitet för substitut men en negativ för komplement, dvs: ε < 1 : Oelastiskt utbud ε > 1: Elastiskt utbud Exempel: På 80-talet kostade en videofilm 49 kr att hyra. Idag kan man hyra en film för 29 kr i videobutiken. Varför? Idag har vi fler substitut, så måste sänka priset på videouthyrning för att det ska vara intressant. Olika elasticitet på kort sikt och lång sikt. På lång sikt så har man en större anpassning och därmed större elasticitet. Samma för både efterfrågan och utbudet. Konsumenternas valUtgörs av:
Dessa två är villkor för nyttomaximering och utgiftsminimering. NyttofunktionerEn nyttofunktion u(q1, q2) tilldelas varje varukorg ett visst värde. Värdet av u ökar i q1 och q2. M.h.a u(q1, q2) kan vi ranka alla varugorgar så att vi vet att A > B om ua > ub => u är en ordinal funktion, men vi kan inte säga med hur mycket. Motsatsen är en kardinal funktion där vi också vet hur mycket mer man värderar en sak än en annan. T.ex. pengar mäts kardinalt. Eftersom u(q1, q2) är ordinal ges den samma ranking av vaugorgar som v = F(u(q1, q2)) där F är en positiv monoton transormation. u = q1α, qbβ och v = 3 * u = 3 * q1α, qbβ v = ln * u = ln(q1α, qbβ ) = α * ln q1 + β * ln q2 Varje varukorg har ett visst värde: u(q1, q2). Alla varukorgar med samma värde kan ritas upp längs samma indifferenskurva. Från Wikipedia (I det här fallet utgår vi ifrån att vara X = q1 och vara Y = q2 och att l1, l2, l3 = u0, u1, u2) Regler:
Lutning på indifferenskurva: Hur mycket av q2 är vi villiga att ge upp för en extra enhet av q1? Denna kvor kallas marginell substitutionskvot: MRS Hur mycket q2 är vi villiga att avstå från för en extra enhet av q1? Om vi ökar den ena varan så ökar nyttan. ∂u/∂q1 = marginalnyttan (MU) av q1 ∂u/∂q2 = MU2 (marginalnyttan av q2) Om vi ökar q1, med hur mycket ska q2 ändras för att nyttan ska vara konstant, detta skrivs som: u(q1, q2) = û (egentligen rakt streck ovanför)? Vi kan skriva om nyttofunktionen: u(q1, q2(q1)) = û Lutningen på indifferenskurvan: dq2/dq1 Vi deriverar u(q1, q2(q1)) med avseende på q1. Vi definierar den till 0 eftersom vi inte vill ändra nyttan. ∂u/∂q1 + ∂u/∂q2 * dq2/dq1 = 0 Vi vill nu lösa ut dq2/dq1: dq2/dq1 = -(∂u/∂q1) / (∂u/∂q2) dq2/dq1 = - MU1/MU2 dq2/dq1 = MRS Detta är lutningen på indifferenskurvan BudgetrestriktionVi utgår ifrån att vi alltid vill konsumera för all vår inkomst (icke-mättnadskriterium) så vår inkomst (Y) läggs på att köpa en viss kvantitet av olika varor (q1, q2 osv) för ett visst pris (P1, P2 osv). Vi får då: P1q1 + P2q2 = Y Hur mycket mindre q2 kan vi köpa om vi köper 1 enhet till av q1? Lutning på budgetrestriktionen. Vi måste derivera med avseende på q1. q2 är beroende av q1 eftersom vid en given nivå av q1 så måste q2 vara ett visst värde. Vi får därför: P1 + P2 * (dq2)/(dq1) = 0 Omskrivet: (dq2)/(dq1) = -P1/P2 Denna kallar vi för den marginella transformationskvoten (MRT). Hur mycket måste vi avstå från q2 för att ha råd med en extra enhet q1? NyttomaximeringVi vill maximera nyttan givet vår budgetrestriktion, dvs nå en indifferenskurva så långt från origo som möjligt. Måste därför sätta ihop vår nyttofunktion och vår budgetrestriktion. Den röda linjen utgör budgetrestriktionen, och de blå indifferenskurvor. Den maximala nyttan uppnås där budgetrestriktion och indifferenskurva tangerar varandra, dvs att de har precis samma lutning (vid punkten T i bilden ovan). Lutningarna har vi från tidigare: MRS och MRT. Dessa definierades som: MRS = -MU1/MU2 MRT = -P1/P2 Vi når alltså nyttomaximering när: MRS = MRT Samma som: -MU1/MU2 = -P1/P2 Vi kan även skriva om detta: MU1/P1 = MU2/P2 MU1/P1 visar marginalnyttan av vara 1 genom priset av vara 1. Dvs, hur mycket extra nytta får jag om jag lägger en extra kr på vara q1? Det är just när jag inte kan öka min nytta ytterligare genom att lägga pengar på den andra varan som vi nåt nyttomaximering. Dvs när en extra krona på q1 ger lika stor nyttoökning som en extra krona på q2. HörnlösningDet finns fall när vi inte finner någon positiv tangeringspunkt och MRS inte är lika med MRT. Detta kallas för hörnlösning innebär att vi enbart bör köpa den ena varan för att maximera vår nytta. Om vi t.ex. har väldigt flacka indifferenskurvor och en väldigt brant budgetrestriktion, då skulle vi få en tangeringspunkt när q1 är negativ. Detta innebär att vi endast bör köpa q2 (vi sätter q1 = 0). Nyttomaximering - matematisktMaximering av nyttofunktionen: u(q1, q2) givet budgetrestriktionen: P1q1 + P2q2 = Y Lättast är att sätta upp en lagrange-funktion: λ - Lambda. Marginalnyttan av inkomsten (se nedan) max L = u(q1, q2) + λ(Y - P1q1 - P2q2) q1, q2, λ Vi deriverar L med avseende på q1: ∂L/∂q1 = ∂u/∂q1 - λP1 = 0 (1) Vi deriverar L med avseende på q2: ∂L/∂q2 = ∂u/∂q2 - λP2 = 0 (2) Vi deriverar sen L med avseende på lambda: ∂L/∂λ = Y - P1q1 - P2q2 = 0 (3) Utnyttja (1) och (2). Vi skriver om dem: (1): ∂u/∂q1 = λP1 (2): ∂u/∂q2 = λP2 Vi kan sen dividera bägge leden: (∂u/∂q1) / (∂u/∂q2) = (λP1) / (λP2) Vi kan stryka lambda Vi ser nu att vänsterledet är -MRS och högerledet är -MRT. Vi har fått fram nyttomaximeringsekvationen MRS = MRT Vad är lambda exakt? Vi löser ut lambda från ekvation (1); ∂L/∂q1 = ∂u/∂q1 - λP1 Vi får ut: λ = MU1 / P1 För ekvation (2) får vi: λ = MU2 / P2 Detta är alltså marginalnyttan av en viss vara om vi lägger en extra krona på det. Lambda är ett mått på hur mycket vår nytta ökar om vi får en extra krona. Marginalnyttan av inkomsten. Detta är generella ekvationer. Specifikt exempel: Nyttofunktionen: u = q11/2, q21/2 Budgetrestriktion: P1q1 + P2q2 = Y Hur mycket q1 resp q2 efterfrågas om vi maximerar u givet budgetrestriktionen? Lagrange: L = q11/2 * q21/2 + λ(Y - P1q1 - P2q2 ) Vi deriverar med avseende på q1: ∂L/∂q1 = 1/2 * q11/2-1 * q21/2 - λ * P1 = 0 (1) Vi deriverar med avseende på q2: ∂L/∂q2 = 1/2 * q11/2 * q2-1/2 - λ * P2 = 0 (2) Vi deriverar med avseende på lambda: ∂L/∂λ = Y - P1q1 - P2q2 = 0 (3) λ = (1/2 * q11/2 * q2-1/2 ) / P2 Utnyttja i (1): 1/2 * q1-1/2 * q21/2 - (1/2 * q11/2 * q2-1/2 ) / P2 * P1 = 0 Vi kan flytta om: 1/2 * q1-1/2 * q21/2 = 1/2 * q11/2 * q2-1/2 * P1 / P2 Vi delar med 1/2 på bägge sidor: q1-1/2 * q21/2 = q11/2 * q2-1/2 * P1 / P2 Vi delar med (q11/2 * q2-1/2): (q1-1/2 * q21/2 ) / (q11/2 * q2-1/2 ) = P1 / P2 Summan av vänsterledet ger oss: q2 / q1 = P1 / P2 Samma som: P1 * q1 = P2 * q2 Kan utnyttja P1 * q1 = P2 * q2 i budgetrestriktionen: p1q1 + p1q1 = 2p1q1 = Y Av detta får vi en efterfrågefunktion: q1 = Y/(2P1) Pga symmetri: q2 = Y/(2P2) Jfr i boken Solved problem 3.2 Dessa beräkningar kan även användas för att nå en viss nyttonivå, t.ex. existensminimum. UtgiftsminimeringVi kan istället minimera utgifterna givet att vi vill uppnå en viss nyttonivå. Detta kommer vi att hitta i exakt samma punkt, så resultatet kommer bli detsamma. Minimera utgifterna (E): E = P1q1 + P2q2 givet att vi använder en specifik nyttofunktion: u(q1, q2) = û (ett specifikt värde av u) Specifikt exempel: u = q11/2, q21/2 Vi sätter även här upp en Lagrange-ekvation, men vill istället minimera: L = P1q1* P2q2 + λ(û - q11/2 * q21/2 ) Restriktionen skiljer sig ifrån nyttomaximering Vi deriverar med avseende på q1. Vi får -1 på exponenten av q1 eftersom det är den vi deriverar med avseende på, medan q2:s exponent lämnas i fred eftersom q2 klassas som en konstant: ∂L/∂q1 = P1 - λ * 1/2 * q1-1/2 * q21/2 = 0 (1) Vi deriverar med avseende på q2: ∂L/∂q2 = P2 - λ * 1/2 * q11/2 * q2-1/2 = 0 (2) Vi deriverar med avseende på lambda: ∂L/∂λ = û - q11/2 * q21/2 = 0 (3) Vi skriver om ekvation (1) och (2) (1): P1 = λ * 1/2 * q1-1/2 * q21/2 (2): P2 = λ * 1/2 * q11/2 * q2-1/2 Vi får ut: P1/P2 = (λ * 1/2 * q1-1/2 * q21/2 ) / ( λ * 1/2 * q11/2 * q2-1/2 ) P1/P2 = q2 / q1 Samma som: -MRT = -MRS Hur mycket q1 och q2 efterfrågas till priserna P1 och P2 om vi vill uppnå nyttan û? P1q1 = P2q2 q2 = (P1q1) / P2 Substituerar in detta i nyttofunktionen (u): u = q11/2 * q21/2 = û û = q11/2 * ( (P1q1) / P2)1/2 Kan förenkla: û = (q11/2 * P11/2 *q11/2 ) / P21/2 û = (q1 * P11/2 ) / P21/2 Vi får: q1 = (û * P21/2 ) / P11/2 Detta är en s.k. kompenserad efterfrågefunktion Pga symmetri får vi den kompenserade efterfrågan för q2: q2 = (û * P11/2 ) / P21/2 Vi är nu intresserade av vad det kostar att uppnå en viss nyttonivå. Detta kan vi få fram genom en s.k. utgiftsfunktion. UtgiftsfunktionVad är den minsta kostnaden för att uppnå en specifik nyttonivå (û)? Utgifterna (E) utgörs av: E = P1q1 + P2q2 Specifikt exempel som fortsättning av tidigare del: Vi sätter in den kompenserade efterfrågefunktionen istället för q1 och q2: E = P1q1 + P2q2 E = P1 * ((û * P21/2 ) / P11/2 ) + P2 * ((û * P11/2 ) / P21/2 ) Vi förenklar: E = P11/2 * û * P21/2 + P21/2 * û * P11/2 E = 2û * P11/2 * P21/2 Detta är en utgiftsfunktion Efterfrågefunktioner och elasticiteterEfterfrågefunktioner q(P,Y)Vad händer med q när Y ändras? Vad händer med q när P ändras? Kompenserade efterfrågefunktion q(P, u) Välfärdseffekter när P ändras Inkomstelasticitetξ1 = (% förändring i q1) / (% förändring i Y) = ∂q1 / ∂y * Y/q1 ξ > 0 = Normal vara 0 < ξ < 1 = Nödvändig vara ξ > 1 = Lyxvara ξ < 0 = Inferiöra varor Vi kan ha en mix av normala och inferiöra varor, men alla varor kan inte vara inferiöra. Vad händer med total konsumtion när y ökar? P1q1 + P2q2 + ... Pnqn = Y Derviera m.a.p. Y qi = D(P1, ..., Pn, Y) P1 * ∂q1 / ∂Y + P2 * ∂q2 / ∂Y + .... + Pn ∂qn / ∂Y = 1 P1q1 / Y * ∂q1/∂Y * Y/q1 + P2q2 / Y * ∂q2/∂Y * Y/q2 + ... + Pnqn / Y * ∂qn/∂Y * Y/qn = 1 Inkomstandelen för q1 utgörs av P1q1 / Y (vi kallar detta θ) och ∂q1/∂Y * Y/q1 är elasticiteten (som vi kallar för ξ) θ1 * ξ1 + θ2 * ξ2 + ... + θn * ξn = 1 Summan av alla inkomstelasticiteter viktade med inkomstandelarna ska summera till 1. Priselasticitet(?)Om vi utgår ifrån en indifferenskurva + budgetrestriktion. Om priset på vara q1 sjunker för en vara så får vi en ny jämvikt, eftersom lutningen på budgetrestriktionen ändras (vi kan nu köpa mer av vara q1). Vi får en ny tangeringspunkt vid en högre indifferenskurva. Två effekter:
Vi kan kombinera denna med den kompenserade efterfrågefunktionen: Till vänster - indifferenskurva och budgetrestriktion, till höger - vanlig efterfrågekurva och kompenserad efterfråga. Stämmer denna bild?? H(P, u0) : Kompenserad efterfråga (Hicks kompenserade efterfråga). Den kompenserar för den förlorade köpkraften när P stiger och tar bara hänsyn till substitutionseffekten. Längs denna finns de kombinationer av q och p som gäller om nyttonivån (u0) ska vara konstant. Vi har alltså den totala efterfrågan, som är en funktion av priser och en viss inkomst. q1 = D(P1, P2, Y) Om P1 ändras så ändras D p.g.a. både inkomst- och substitutionseffekt. Vi har även den kompenserade efterfrågan (H), som är en funktion av priser och en viss nyttonivå (û): q1 = H(P1, P2, û) Om P1 ändras så ändras H bara p.g.a. substitutionseffekten. Utgiftsfunktion (vi kallar den E): Vad kostar det att uppnå en viss nyttonivå (û)? E(P1, P2, û) = P1 * H1(P1, P2, û) + P2 * H2(P1, P2, û) Vad händer när P1 ökar marginellt? q1 = D(P1, P2, Y) Vi kan skriva om efterfrågefunktionen genom att byta ut Y (inkomsten) till vår utgiftsfunktion (E) q1 = D(P1, P2, E(P1, P2, û)) Detta är detsamma som att skriva: q1 = H(P1, P2, û) Den kompenserade efterfrågan är samma som den totala efterfrågan när vi substituerar in utgiftsfunktionen i Y. H(P1, P2, û) = D(P1, P2, E(P1, P2, û)) Om vi deriverar detta med avseende på P1 så får vi: ∂H / ∂P1 = ∂D / ∂P1 + ∂D / ∂Y * ∂E / ∂P1 Vi ser att derivatan ∂E / ∂P1 är samma som q1 Vi kan skriva om ovanstående till: ∂D / ∂P1 = ∂H / ∂P1 - ∂D / ∂Y * q1 Det vi fått ut är ett centralt samband som kallas för Slutskyekvationen Vad händer med den totala efterfrågan när priset ändras? ∂D / ∂P1 Vi har både en substitutionseffekt: ∂H / ∂P1 Och en inkomsteffekt: ∂D / ∂Y * q1 Vi kan även uttrycka detta i elasticitetsform, genom att multiplicera allt med P1 / q1: ∂D / ∂P1 * P1 / q1 = ∂H / ∂P1 * P1 / q1 - ∂D / ∂Y * q1 * P1 / q1 Vänsterledet ∂D / ∂P1 * P1 / q1 är den klassiska efterfrågeelasticiteten som vi brukar kalla för epsilon (ε) Nästa term ∂H / ∂P1 * P1 / q1 utgör istället den kompenserade efterfrågeelasticiteten (substitutionseffekten), som benämns εc. Den sista termen behöver vi skriva om lite: ∂D / ∂Y * q1 * P1 / q1 ∂D / ∂Y * Y / q1 * (q1P1) / Y Vi ser att den första termen ∂D / ∂Y * Y / q1 är inkomstelasticiteten (ξ) och att den andra är inkomstandelen (θ) Vi kan alltså sammanfatta den ursprungliga elastitietsekvationen till: ε1 = ε1c - ξ1 * θ1 Den kompenserade effekten/Substitutionseffekten (ε1c) är alltid negativ. Inkomstelasticitet/-andel (ξ1 * θ1) kan vara positiv eller negativ, beroende på om det är en normal vara eller ej. VälfärdseffekterUtgår ifrån en vanlig efterfrågafunktion (D) Varje punkt på D mäter marginell betalningsvilja. Från första punkten är man villig att betala jättemycket för väldigt lite av varan, nästa punkt betala lite mindre för lite mer, osv. Men vi har ett jämviktspris (P*) och en jämviktskvantitet (q*) som är beroende av utbudet. Ytan ovanför P* är ett konsumentöverskott (CS, consumer surplus) eftersom man bara behöver betala p* för samtliga enheter trots att man är villig att betala mer per enhet. Konsumentöverskottet visar hur mycket vi slipper betala (per transaktion?). Om jämviktspriset (P*) ändras (i bilden från C till B) kommer konsumentöverskottet (CS) också att ändras (i bilden: från 1+2+3 till 2). Om t.ex. P* höjs så kommer den efterfrågade kvantiteten (q*) att minska (i bilden från H till F), och vi får en minskning av konsumentöverskottet, som kan delas upp i två effekter: 1) Minskad konsumtion (i bilden 3) 2) Högre pris på den konsumerade kvantiteten (i bilden 1) Formellt (s är egentligen en konstig symbol): ΔCS = -s2010 * 100/P * dP ΔCS = -[100 ln P]2010 ΔCS = 100(ln 10 - ln 20) = ca -69 ΔCS innehåller både en inkomst- och en substitutionseffekt. För att fånga substituionseffekten krävs alternativa mått. Den kompenserade efterfrågan visar efterfrågan om vi vill behålla samma nyttonivå. För att få ett korrekt mått på hur mycket individen förlorar när priset ökar så är CV (Compensated Variation) det mått vi bör använda. Vi vet aldrig folks egentliga, men däremot kan vi mäta förändringar i köpbenägenhet hos konsumenter, dvs mäta den totala efterfrågan. Om varan däremot utger en liten del av vår budget och inkomsteffekterna är små så kan vi använda konsumentöverskottet (ΔCS) som approximation. Men ΔCS är alltid en underskattning av konsumenternas välfärdsförlust. CV och EV är däremot användbara när vi värderar varor som inte finns på marknader, t.ex. kollektiva varor. Man kan t.ex. göra undersökningar där man frågar folk om deras betalningsvilja. Används t.ex. mycket i miljöekonomi. Kompenserad efterfråga - repetitionHur mycket efterfrågas vid givna priser för att uppnå en viss nytta (û), dvs ligga kvar på samma indifferenskurva? Nyttofunktion: u = q11/2 + q21/2 Budgetrestriktion: E = P1q1 + P2q2 Vi vill minimera utgifterna för ett givet û. Vi sätter upp en Lagrange-ekvation: L = P1q1 + P2q2 + λ(û - q11/2 - q21/2 ) Restriktionen skiljer sig ifrån nyttomaximering Vi deriverar med avseende på q1. Vi får -1 på exponenten av q1 eftersom det är den vi deriverar med avseende på, medan q2:s exponent lämnas i fred eftersom q2 klassas som en konstant: ∂L/∂q1 = P1 - λ * 1/2 * q1-1/2 * q21/2 = 0 (1) Vi deriverar med avseende på q2: ∂L/∂q2 = P2 - λ * 1/2 * q11/2 * q2-1/2 = 0 (2) Vi deriverar med avseende på lambda: ∂L/∂λ = û - q11/2 * q21/2 = 0 (3) Vi skriver om ekvation (1) och (2) (1): P1 = λ * 1/2 * q1-1/2 * q21/2 (2): P2 = λ * 1/2 * q11/2 * q2-1/2 Vi får ut: P1/P2 = (λ * 1/2 * q1-1/2 * q21/2 ) / ( λ * 1/2 * q11/2 * q2-1/2 ) Kan skriva om: P1/P2 = q21/2 / q1-1/2 Kvadrera (upphöjt i två i bägge leden) och flytta om: q2 = (P1/P2)2 * q1 Kan substituera in i nyttofunktionen för att få ut en specifik nyttonivå (û): u = q11/2 + q21/2 û = q11/2 + ((P1/P2)2 * q1)1/2 û = q11/2 + (P1/P2) * q11/2 û = q11/2 * ((P1+P2 / P2) q11/2 = (û * P2) / (P1+P2) Vi får den kompenserade efterfrågan för q1: q1 = û2 * P22 / (P1+P2)2 Kan göra samma sak för q2: q2 = û2 * P12 / (P1+P2)2 Vad blir våra utgifter för att uppnå en viss nyttonivå (û)? Utgifterna (E) = P1q1 + P2q2 E(P1, P2, û) Genom att substituera in våra kompenserade efterfrågefunktioner så får vi fram den konkreta utgiftsfunktionen: E = P1q1 + P2q2 E = P1 (û2 * P22 / (P1+P2)2 ) + P2 (û2 * P12 / (P1+P2)2 ) Kan förenklas: E = (P1 P2 û2 ) / (P1 + P2)2 (P1+P2) Eftersom vi har (P1+P2) i kvadrat så kan vi stryka en (P1+P2): E = (P1 P2 û2 ) / (P1 + P2) Detta är vår utgiftsfunktion. ArbetsutbudVi får nytta av:
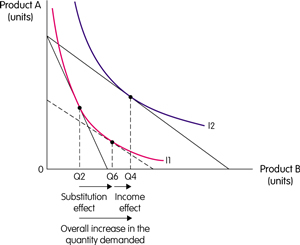
Vi kan sätta upp detta i en indifferens-/nyttofunktion: u = u(Y, N) Vår budgetrestriktion utgörs av vår inkomst, dvs: Y = w * H + Y* Vi har även en tidsrestriktion, som utgörs av antal arbetade timmar (H): Vi kan nu substituera in dessa i nyttofunktionen: u = u(Y, N) u = u(w * H + Y*, 24 - N) Hur mycket ska man jobba? Vi vill derivera nyttofunktionen med avseende på H och ta reda på när derivatan är 0: du/dH = 0 Detta ger oss: ∂u/∂Y * w - ∂u/∂N = 0 Kan skrivas om: (- ∂u/∂N) / (∂u/∂Y) = -w/1 Vi har nu i en kvot mellan två marginalnyttor i vänsterledet. Dvs den marginella substitutionskvoten (MRS) mellan fritid och inkomst. I högerledet har vi istället MRT för fritid och inkomst, dvs priset på fritid, hur mycket det kostar oss att ta ut mer fritid. Exempel: Utgår ifrån att: u = Konsumtion (C) + ln N C = Arbetade timmar (H) * Lön (w) N = 24 - H Vår nyttofunktion blir: u = H * w + ln(24 - H) Hur mycket ska man jobba? Deriverar nyttofunktionen med avseende på H: du/dH = w - 1/(24 - H) Vi sätter derivatan till 0 eftersom vi vill finna det optimala valet: w - 1/(24 - H) = 0 Vi löser nu ut H (antal arbetade timmar): 24 - H = 1/w H = 24 - 1/w Detta ger oss svaret på hur många timmar vi bör arbeta, och vi ser att det beror på vilken lön man får. Vad händer med arbetsutbudet (H) om lönen (w) ökar? Vi deriverar H med avseende på w: dH/dw = 1/w2 Eftersom 1/w2 alltid är positivt så kan vi dra slutsatsen att vi alltid kommer att jobba mer med en högre lön. Vi kan även ta reda på den s.k. reservationslönen (w0), dvs den lägsta lönen man kan tänka arbeta för. Vi använder arbetsutbudsekvationen fast utgår ifrån reservationslönen, och tar reda på när den är 0: 24 - 1/w0 = 0 w0 = 1/24 Detta ger oss reservationslönen, dvs om lönen är mindre än 1/24 så har vi ingen nytta av att jobba i det här fallet. Inkomst-/substitutionseffektPrecis som tidigare kan vi även här delar upp förändringar i arbetsutbudet i både en inkomst- och substitutionseffekt. Vi ritar upp en indifferenskurva tillsammans med en tangerande budgetrestriktion precis som förut, men även en vertikal tidsrestriktion. Om lönen (w) ökar så måste vi öka budgetrestriktionen, och vi får nu en ny jämvikt när den tangerar en högre indifferenskurva. Förändringen kan delas upp i inkomst- och substitutionseffekt. Substituionseffekten innebär att vi fått mindre N och mer Y, att fritiden relativt sett blivit dyrare. Detta gör att man vill jobba mer. Inkomsteffekten: Vi konsumerar mer av N eftersom vi har mer inkomst. Man behöver inte jobba lika mycket. Detta gör att vi vill jobba mindre. Två motverkande effekter. Totaleffekten beror på vilken av dessa två som är starkast. Om inkomsteffekten dominerar så kommer man att jobba mindre om lönen ökar, medan om substitutionseffekten så kommer vi att jobba mer. Praktiskt exempel Inkomstelasticitet (Inkomsteffekt) Kompenserad löneelasticitet (Substitutionseffekt) Män -0,1-0,0 0,08-0,24 Kvinnor -0,24- -0,03 0,22-1,07 Kvinnors arbetsutbud mer lättpåverkat. Gifta kvinnors arbetsutbud påverkas av deras mäns inkomster. Män däremot opåverkade av sina fruars inkomster. Källa: Agell m.fl (1995), Svensk ekonomi (2008) Sådana här uppgifter kan t.ex. användas för att förutsäga effekter av jobbskatteavdrag. Kan se en stark substitutionseffekt hos låginkomsttagare, medan främst män med högre inkomster domineras av inkomsteffekten, och vi får t.o.m. negativ effekt av jobbskatteavdrag. Kritik Stämmer det att det kalkylerade arbetsutbudet är samma som faktiskt arbetade timmar? Inte nödvändigtvis, eftersom det finns flera aspekter som modellen inte tar hänsyn till:
OsäkerhetSka man köpa ett paraply, vilken aktie ska man välja osv, alla exempel på osäkerhet. Variabler: Vi = Olika utfall θi = Sannolikheten att utfallen inträffar u = Nytta Eu = Förväntad nytta (Expected utility) Eu = Summa(n, i=1) * θi * u(Vi) Exempel: u = Y1/2 Y är osäker. Med 40% sannolikhet (θ1 = 0,40) blir Y = 100 och med 50% sannolikhet (θ2 = 0,6) blir Y = 50 Eu = 0,4 * 1001/2 + 0,6 * 501/2 Eu = 8,24 Detta ger oss den förväntade nyttan. Detta är inte samma sak som nyttan (u(EY)) av den förväntade inkomsten (EY), vilket snarare skulle varit: EY = 0,4 * 100 + 0,6 * 50 EY = 70 u(EY) = 701/2 u(EY) = 8,37 Vi ser att den förväntade nyttan är mindre än den faktiska nyttan av den förväntade inkomsten, dvs: Eu < u(EY) Anledningen att det ser ut så här är för att vi har: Riskaversion - Motvilja att ta risker. En riskavert person är inte villig att ta på sig risker utan kompensation. T.ex. så kanske man hellre vill ha 50kr säkert än 0 resp 100 kr med 50% sannolikhet var. I fallet ovan så representerar Eu en säker inkomst som ger samma nytta som det osäkra utfallet. Avståndet mellan punkterna C och A ovan är det som utgör en riskpremie. Riskpremie - Avgör hur mycket man vill betala för att undgå risk. Riskpremiens storlek avgör hur riskavert man är, vilket i sin tur avgörs av hur konkav nyttofunktionen är. Riskneutral: Man är indifferent mellan säkert och osäkert utfall med samma E(Y). T.ex. företag. Riskbenägen: Man väljer hellre det osäkra utfallet. Riskavert: Man väljer hellre det säkra före det osäkra. De flesta är riskaverta. Arrow-Pratts mått på absolut riskaversion w = wealth U(w) = Nyttan av förmögenheten ρ = Mått på den absolut riskaversionen ρ = -(d2u/dw2) / (du/dw) Om ρ > 0 så är man riskavert Exempel: u = ln w Vi räknar ut delarna av ρ: du / dw = 1/w d2u/dw2 = -1/w2 Vi räknar ut ρ: ρ = 1/w2 ρ = 1/w Vi ser att ρ är avtagande i w. Vi är alltså mer riskaverta för små summor än för stora. Vi har 100 kr och med sannolikheten 20% (θ1 = 0,2) förlorar vi hälften och 80% att vi får behålla dem. Vår nytta utgörs av: u = ln w Hur stor försäkring bör vi köpa? Svar: Vi räknar ut den förväntade nyttan utan försäkring: E[u] = 0,2 * ln 50 + 0,8 * ln 100 E[u] = 4,47 Vi nu har möjlighet att köpa en försäkring. Vi måste betala en premie, P, och får en ersättning, G, om vi förlorar hälften av pengarna. För att försäkringsbolaget ska gå runt måste de gå plus/minus noll, dvs P = 0,2G Vår förväntade nytta med försäkringen blir således (-0,2G som kostnaden för premien): E[u] = 0,8 ln(100 - 0,2G) + 0,2 ln(50 + G - 0,2G) Vi deriverar detta: ∂E[u] / ∂G = (-0,8 * 0,2) / (100 - 0,2G) + (0,2 * 0,8G) / (50 + 0,8G) Detta ska vara 0: (-0,8 * 0,2) / (100 - 0,2G) + (0,2 * 0,8G) / (50 + 0,8G) = 0 Löser ut G: G = 50 Om G är 50 så vill vi teckna full försäkring(?) ProduktionsteoriIsokvanterAntaganden
Mått på substituerbarhet Marginella tekniska substitutionskvoten (MRTS) - Lutningen på isokvanten Liknande MRS som är lutningen på nyttofunktionen, men "tekniska" betonar att det rör sig om produktion och inte konsumtion. MRTS = ΔK/ΔL = dK/dL Produktionsfunktionen: q = f(K, L) Vi bestämmer att vi ska ligga på en specifik kvantitet (q) q = f(K(L), L) dq / dL = 0 = ∂f/∂L + ∂f/∂K * dK/dL Kan flytta om dK/dL = -(∂f/∂L / ∂f/∂K) Detta är samma som: MRTS = -MPL / MPK MRTS = Marginalprodukten av arbete / marginalprodukten av kapital Ex. MRTS och Cobb-Douglas q = ALaKb Ska räkna ut MRTS genom att derivera uttrycket MPL = ∂q/∂L MPL = AaLa-1Kb MPK = ∂q/∂K MPK = ALabKb-1 MRTS = MPL/MPK MRTS = (ALabKb-1 ) / ALabKb-1 ) Stryker A, stryker exponenten a och exponenten b. MRTS = -(a*K)/(b*L) Om a och b är identiska kan vi även stryka dem, t.ex. om a = b = 0.5 så skulle vi få MRTS = -K/L SkalavkastningStordriftsfördelar / Skalavkastning / Returns to scale Hur mycket förändras produktionen då alla insatsfaktorer i samma proportion. Ofta på lång sikt. Exempel på konstant skala: Vi utgår ifrån en enkel isokvant: q = K + L För att testa stordriftsfördelar ökar vi K och L lika mycket, t.ex: q = 2K + 2L q = 2(K + L) = 2q Produktionen fördubblas. Då båda faktorerna ökar med en faktor 2 så ökar produktionen med lika mycket. Är detta stordriftsfördelar? Nej, detta är en konstant skala. Exempel på skalavkastning: q = K2 + L2 Vi testar stordriftsfördelar genom att öka båda produktionsfaktorerna: q = (2K)2 + (2L)2 q = 22 (K2 + L2 ) q = 4 - q Då faktorerna ökar med en faktor 2 så ökar q med en faktor 4. Detta är stordriftsfördelar / ökande skalavkastning eftersom vi får mer än en fördubbling i ökad produktion. Exempel på stordriftsnackdelar: q = K0.5 + L0.5 ... (samma beräkningar som tidigare) Om K och L ökar med 2 så ökar q med roten ur 2. Detta är stordriftsnackdelar / avtagande skalavkastning eftersom vi får mindre än en fördubbling i ökad produktion. I praktiken brukar växande företag få avtagande skalavkastning. Anledningen är att de blir svårare att styra och svåröverblickbara. Dvs man kan få stordriftsfördelar i produktionsteknologi, men samtidigt växande stordriftsnackdelar i styrning och organisation. Kan vara så att man inom en produktionsenhet kan få både ökande och konstant skalavkastning inom olika delar av enheten. Olika effekter beroende på vilken producerad kvantitet man tittar på. Kan t.ex. se en produktionsprocess där man vid en ökning av små kvantiteter så har vi ökande skalavkastning, ökning i medelstora så har vi konstant skalavkastning, ökning i stora kvantiteter så får vi avtagande skalavkastning. Sammanfattning: f(K, L) Ökningsfaktor (x) > 1 f(xK, xL) = xγ * f(K, L) γ (gamma) = 1: Homogen av grad 1 dvs konstant skala γ > 1: Homogen av grad > 1 dvs ökande skalavkastning γ < 1: Homogen av grad < dvs avtagande skalavkastning Val i utbildningenVal mellan: Finansiell ekonomi - Isf, välja corporate finance Nationalekonomi i allmänhet - Välj makro Val termin 6 (termin 3 för fristående): Obligatorisk kurs oavsett inriktning - Basic econometrics De som väljer finans ska också läsa portfolio investments De som väljer andra inriktningar så finns några olika val som lämpligen (men inte nödvändigtvis) sen lägger grunden till kandidatuppsatsen: Miljöekonomi Utvecklingsekonomi Economic policy and individual behavior - Utvärderingsproblematik, utvärderar projekt i offentlig sektor, cost-benefit. Även mikrobaserad fördjupning, beteendeekonomi osv. T.ex. viktigt med relativa förhållanden i resursfördelning / nyttomaximering osv. Avslutas med kandidatuppsats - 15 hp, 10 veckor Plocka ut kandidat - 180 hp Antingen ekonomiekandidat - 90 hp nationalekonomi, 30 hp företagsekonomi, 15 hp statistik, 45 hp valfritt Eller filosofiekandidat - 90 hp nationalekonomi, 90 hp valfritt (varav 15 hp statistik för att komma in på master) Härifrån går vissa vidare till arbetslivet eller masterprogram lokalt eller internationellt Master i gbg - 2-årig fördjupning. Kräver någon form av kandidat (inkl färdig kandidatuppsats), plus ett test i GMAT. Likt högskoleprovet, testar mattekunskaper, logik osv. GMAT kostar $250 att göra? Kan endast göras om en gång var femte år? Läs mer här: Detaljer om HHGS master-utbildningen: Statistik 15hp obligatoriskt för master (egentligen minimum 7.5 hp i econometretrics och 7.5 hp statistik?) Fördjupningskurser på master-nivå: Hälsoekonomi Utvecklingsekonomi Finans Offentligekonomi m.m. ProduktionsteoriKostnader på kort siktSamband mellan produktion och kostnader på kort sikt L rörlig faktor och priset är w K fast faktor vid K priset är r Fasta kostnader = priset på kapital: F = rK Variabla kostnader = priset på arbetskraft: VC = wL Produktionsfunktion: q = f(K, L) Vi har en fast nivå på K: q = f(K, L) När vi gör en faktor fast så kan vi stryka den faktorn ut funktionen, eftersom den inte längre behöver kunna ändras. Kan istället skriva: q = g(L) Kan skrivas om som invers funktion: L = g-1(q) Vi kan nu sätta in våra funktioner för fasta och variabla kostnader här: VC(q) = w * g-1(q) Marginalkostnaden, vi vet att den är derivatan av de totala kostnaderna: MC = dC(q) / dq Men eftersom de fasta kostnaderna inte förändras (dF/dq = 0) så kan vi bortse från dessa och bara räkna på de variabla kostnaderna: MC = dVC(q) / dq Vilket är detsamma som: MC = w * dL/dq Kan skrivas om MC = w / (dq/dL) Vi brukar benämna (dq/dL) som marginalprodukten av arbetskraft (MPL), så vi har: MC = w/MPL Kurvan är u-formad. Lagen om marginellt avtagande avkastning. Exempel: På kort sikt: En klassisk Cobb-Douglas funktion f(K, L): q = K0.5 * L0.5 Vi har en viss nivå av kapital: K = 81 Vi kan då skriva: q = 810.5 * L0.5 q = 9L0.5 Vi kan kalla denna funktionen för g(L) L0.5 = 1/q * q L = 1/81 * q2 Vi kan sätta in detta i vår funktion för variabla kostnader: VC(L) = w * L VC(q) = w * g-1(q) VC(q) = 1/81 * q2 Med inga "fasta kostnader" menas egentligen inga "sunk costs". Dvs, kostnader som är förlorade som man aldrig kan få tillbaka genom att ex. sälja. Dessa finns inte på lång sikt. Kostnader på lång siktInga fasta kostnader. Utgår ifrån isokostlinjen (precis som budgetlinjen): C = wL + rK Vi jobbar med endast två variabler i dessa förenklade exempel, men det är inget som hindrar oss från att använda fler i verkligheten. Kan skriva om kostnadsfunktionen: rK = C - wL K = C/r - w/r * L Exempel: w = $24 r = $8 KonstnadsminimeringLutningen på isokvanten: MRTS = -MPL/MPK Lutningen på isokostlinjen: -w/r Krav för kostnadsminimum: MPL/MPK = w/r Kan sätta upp både kostnadsminimering och kvantitetsmaximering vilka ger samma resultat (precis som nyttofunktionen), men kostnadsminimering känns mest rimligt för företag eftersom det är det realistiska scenariet. Lagrange: Min kostnaden C Bivillkor produktionsfunktionen q = f(K, L) Skapa Lagrangefunktionen: min l(K, L, λ) = wL + rK + λ(q - f(k, L)) K, L, λ Dervierar L: ∂l/∂L = w - λ * ∂f/∂L = 0 Deriverar K: ∂l/∂K = r - λ * ∂f/∂K = 0 Deriverar Lambda: ∂l/∂λ = q - f(k, L) = 0 Löser ut lambda ur första och andra uttrycket och sätter dem lika: Första: w - λ * ∂f/∂L = 0 w = λ * ∂f/∂L w / (∂f/∂L) = λ Uttrycket (∂f/∂L) är samma som marginalprodukten av arbetskraft MPL λ = w / MPL Andra: r - λ * ∂f/∂K = 0 r = λ * ∂f/∂K r / (∂f/∂K) = λ Uttrycket (∂f/∂K) är samma som marginalprodukten av kapital MPK λ = r / MPK Vi sätter uttrycken till varandra: w / MPL = r / MPK Kan lösa ut: w / r = MPL / MPK Vi har nu villkoret för kostnadsminimering. Långsiktig kostnadsfunktionOm man tar tangeringspunkterna för flera isokost- och isokvantkurvor och drar en linje mellan dessa tangeringspunkter får vi den s.k. expansion path / expansionsstigen. Detta ger oss den långsiktiga kostnadskurvan (login-run cost curve), med kostnaden (C) beroende av totala kvantiteten (q). Exempel på långsiktig kostnadsfunktion: min C = wL + rK biv q = f(K, L) = K0.5 * L0.5 Lagrange (l): l(λ, K, L) = wL + rK + λ(q - K0.5 * L0.5 ) min λ, K, L Dervierar L: ∂l/∂L = w - λ * 0.5K0.5 * L-0.5 = 0 Deriverar K: ∂l/∂K = r - λ * 0.5K-0.5 * L0.5 = 0 Deriverar Lambda: ∂l/∂λ = q - K0.5 * L0.5 = 0 Löser ut lambda ur första och andra uttrycket och sätter dem lika: Första: w = λ0.5 * 0.5K0.5 / L-0.5 Löser ut lambda: λ = wL0.5 / 0.5K-0.5 Det under bråket är samma som marginalprodukten av arbetskraft MPL λ = w / MPL Andra: r = λ0.5 * L0.5 / K0.5 Löser ut lambda: λ = rK0.5 / 0.5L0.5 Det under bråket är samma som marginalprodukten av kapital MPK λ = r / MPK Vi sätter uttrycken till varandra: wL0.5 / 0.5K-0.5 = λ = rK0.5 / 0.5L0.5 Kan förenkla: wL / 0.5 = rK / 0.5 Vi kan nu lösa ut L: L = r/w * K och K: K = w/r * L Vi måste nu först sätta in dessa i produktionsfunktionen för att göra dem till en funktion av q, sen efter detta in i kostnadsfunktionen. Vi kan nu sätta in dessa i lambda / produktionsfunktionen: Börjar med att sätta in L: q - K0.5 * L0.5 = 0 q - K0.5 * (r/w * K)0.5 = 0 q - K(r/w)0.5 = 0 K(r/w)0.5 = q K = (w/r)0.5 * q Vi gör likadant med K: q - K0.5 * L0.5 = 0 q - (w/r * L)0.5 * L0.5 = 0 Efter samma uträkning som ovan får vi: L = (r/w)0.5 * q Vi kan nu utgå ifrån isokostfunktionen: C = wL + rK Vi sätter in L och K från ovan: C = w * (w/r)0.5 * q + r * (r/w)0.5 * q Kan förenklas: C = (w * r)0.5 * q + (r/w)0.5 * q C = 2(wr)0.5 * q Detta ger oss kostnadsfunktionen som berättar hur tangeringspunkterna för isokost-/isokvanten genererar olika kostnader för olika kvantiteter. Visar oss hur kostnaden (c) varierar för olika producerade kvantiteter (q) Exempel: w = r = $10 q = 100 Med kostnadsfunktionen: C = 2(wr)0.5 * q Skulle vi få: C = 2(10 * 10)0.5 * 100 C = $2000 Dvs om vi producerar 100 enheter så kommer det kosta $2000 Om vi ändrar q: q = 150 Skulle vi få: C = 2(10 * 10)0.5 * 150 C = $3000 Dvs om vi producerar 150 enheter så kommer det kosta $3000 osv. I detta fallet, med just denna kostnadsfunktionen, ser vi ett linjärt samband. Vi skulle ha konstanta genomsnittskostnader. Konstanta långsiktiga genomsnittskostnader innebär att vi har konstant skalavkastning. Vi kan göra testet för skalavkastning som vi gick igenom tidigare, och ser att den är konstant. Jämvikt på kort och lång siktExempel: Scenario 1: 1) Kortsiktig jämvikt π < 0 2) π < 0 medför att företag lämnar marknaden. Utbjuden kvantitet på marknaden minskar och därmed höjs priset. 3) Prisstegringen på marknaden leder till att de kvarvarande företagens utbjudna kvantitet ökar. 4) Långsiktig jämvikt där π = 0 Scenario 2: 1) Kortsiktig jämvikt π > 0 2) π > 0 medför att företag ger sig in på marknaden. Utbjuden kvantitet på marknaden ökar och därmed sjunker priset. 3) Prissänkningen på marknaden leder till att de ursprungliga företagens utbjudna kvantitet minskar. 4) Långsiktig jämvikt där π = 0 Effektivitet / VälfärdTillämpningar av den perfekta konkurrensmarknadsmodellen. Producent och konsumentöverskott - repetition Konsumentöverskott - Skillnaden mellan konsumenternas betalningsvilja och vad de faktiskt betalar. Producentöverskott - Skillnaden mellan marknadspriset och det lägsta pris som producenterna kan acceptera för att bjuda ut varan Man kan även rita in producentöverskottet i en graf med pris per enhet (P) på vertikal axel och antal enheter producerade (Q) horisontellt. Ytan mellan marknadspriset och marknadsefterfrågan blir producentöverskottet. Ytan under marknadsefterfrågan blir de variable kostnader. Vinst (π) = Intäkter (R) - Kostnader (C) Eftersom: C = VC + F så kan vi även skriva: π = R - VC - F Producentöverskottet (PÖ): PÖ = R - VC MC = dC(q) / dq Eftersom de fasta kostnaderna är oberoende av q så kan vi lika gärna skriva: MC = dV(q) / dq Vi vill få ut arean. Om efterfrågan varit en rät linje kan man räkna ut arean för triangel, men oftast är den inte det. Vi måste då använda integraler. Vi vill integrera 0-q1 för att få ut arean av de variabla kostnaderna: ∫(0 till q1) * MC * dq = V(q) Vi får då ut företagens totala variabla kostnader. Om vi gör ett ingrepp på marknaden kan vi se om PÖ ökat eller minskat, och därmed dra slutsatsen om företagens vinst ökat eller minskat. PÖ praktiskt tillämpbart mått för att få övergrepp över hela marknaders vinstförmåga. Mått på vinstkapaciteten i företag på hela markander. Exempel: Inverterad utbudskurva (S): P = 0.693Q1.32 Utgångsläge: P = $60 Q = 11.6 Priset minskar och ger oss en ny Q: P = $50 Q = 10.5 Hur förändras producentöverskottet? Vi börjar med P = $60 Vi rör oss från 0 till 11.6 (jämviktslinjen 11.6 ∫ (60 - S) * dq 0 Skriver ut utbudsfunktionen (S): 11.6 ∫ (60 - 0.693Q1.32 ) * dq 0 Räknar ut: 11.6 [60Q - 0.693Q1.32 / 2.32 ] 0 Nästa steg: 60 * 11.6 - 0.693 11.62.32 / 2.32 = 449.3 Här har vi mått på: Intäkterna (60 * 11.6) - Variabla kostnaderna (0.693 11.62.32 / 2.32) P = $50 Vi rör oss från 0 till 11.6 (jämviktslinjen 10.5 ∫ (50 - 0.693Q1.32 ) * dq 0 Räknar ut: .... PÖ = 338.7 Slutsatsen blir att PÖ minskar från 449.3 till 338.7, ca 110. Dvs företagens samlade vinster på denna marknad minskar med 110. Detta gäller oavsett hur det går för enskilda företag, eftersom det ger oss den samlade vinstförmågan på marknaden. Vi kan ha både mindre och högre produktion än jämviktsproduktionen. Vid mindre, så produceras mindre än vad som skulle kunna produceras, t.ex. p.g.a. ett monopol. Välfärdsförlust, delvis KÖ och PÖ. Vid högre, så produceras mer än vad man egentligen kan producera, t.ex. p.g.a. externa effekter, dvs kostnader som inte räknas in i produktionen, t.ex. miljöförstöring. Vi får en välfärdsförlust. För att maximera välfärden (= KÖ + PÖ) så krävs att den sista producerade enhetens kostnad på marginalen (producentens marginalkostnad/utbudet) är lika med betalningsviljan för den sista enheten (efterfrågan). Ex. Om Q2 > Q1 där Q1 uppfyller ovanstående villkor så kommer kostnaden överstiga betalningsviljan så är de extra kostnaderna för Q2-Q1 ytorna mellan Q2 och Q1 från P=0 upp till utbudskurvan (i bilden, B+E+H) och de extra intäkterna ytorna från P=0 till efterfrågekurvan (E+H). Kostnaderna överstiger intäkterna med B. T.ex. Taxiutbud: Varje taxibil har en stigande MC som korsar AC som är u-formad. På en reglerad marknad så sätts blir utbudet stigande, och vid en högre efterfrågan blir priset högre. Medan på en marknad med perfekt konkurrens så ökar endast antalet taxibilar, utbudskurvan blir horisontell och priset består trots att efterfrågan stiger. I Sverige nära perfekt konkurrens medan USA och gamla Sverige mer licenssystem. Jordbrukssubvention: Utan ingrepp så skulle vi ha en klassisk jämvikt mellan traditionella utbud och efterfrågekurvor. Men en prisgaranti som ligger högre än jämviktspriset gör att efterfrågan blir mycket lägre och utbudet blir mycket högre, och detta överskott ser staten till att köpa upp. Mycket mindre konsumentöverskott, men PÖ mycket högre. Bönderna tjänar alltså enormt på att ha en sådan här produktion. I praktiken skickar man ut överskottet på världsmarknaden, vilket gör att världsmarknadspriset sjunker och gör att bönder i fattiga länder får det ännu sämre. 1) Konsumenterna i EU får betala högre pris 2) Bönderna i fattiga länder får det sämre MonpolKaraktäriseras av:
Orsaker till monopolbildning:
Monopolistisk konkurrens - Hård konkurrens men med differentieringsmöjligheter som ändå kan leda till vissa monopol. Oligopol - Ett företag med svaga konkurrenter, där de är dominerande i sin bransch, men har viss konkurrens i närliggande. T.ex. Microsoft. Monopol vinstmaximerar (gäller inte alla, t.ex. inte systembolaget): max π(Q) = R(Q) - C(Q) dπ(Q) / dQ = dR(Q) / d(Q) - dC(Q) / dQ = 0 MR MC Vinstmax vid MR = MC Efterfrågan, MR och efterfrågans priselasticitetViktig för att avgöra marknadsmakt. Ofta i utredningssammanhang, t.ex. för företag eller i domstolssammanhang (läses inom industriell ekonomi). Om t.ex. företag gynnas av en sammanslagning. Inverterade efterfrågan Snarare än Q som en funktion av P så har vi P som en funktion av Q, dvs: P(Q) Vi vet att intäkterna är: R(Q) = P(Q) * Q Vi deriverar R för att få marginalintäkterna (MR). Kädjeregeln för derivering: MR(Q) = P(Q) * dQ/dQ + dP(Q)/dQ * Q MR(Q) = P(Q) + dP(Q)/dQ * Q Vi bryter ut P: MR = P(1 + dP/dQ * Q/P) Detta påminner om efterfrågans priselasticitet: ε = dQ/dP * P/Q Vi skriver om MR för att vända på bråken: MR = P(1 + 1/(dQ/dP * P/Q)) Vi har nu fått: MR = P(1 + 1/ε) Vi ser ex. att om ε = -1 (enhetselasticitetet) så skulle vi få MR = 0, vilket stämmer eftersom det är då vi vinstmaximerar. Detta kan ge oss ett mått på marknadsmakt. Men företag vill inte gärna avslöja sina kostnader. Man studerar därför ofta kostnader indirekt, t.ex. genom priset företaget sätter. Lerner-indexet - Mått på marknadsmakt Vi vet att: MR = P(1 + 1/ε) Antag att företaget (t.ex. ett monopol) är vinstmaximerare, dvs: MC = MR Detta ger: MC = P(1 + 1/ε) Vi delar med P: MC / P = 1 + 1/ε Drar av 1: MC/P - 1 = 1/ε Skriver om: 1 - MC/P = -1/ε (P-MC)/P = -1/ε Liknar hur man räknar ut procent. Visar ett relativt förhållande. Vi har elasticiteten, genom att skatta prisförändringar på marknaden, och vi har priset företaget sätter. Vi kan då lösa ut MC ur ekvationen och få en uppfattning om denna. Men det viktiga är elasticiteten, som talar om för oss företagets marknadsmakt. Efterfrågekurvans lutning i den punkt vi befinner oss. Högerledet (-1/ε) utger Lerner-indexet, mellan 0-1, med högre siffror som innebär större marknadsmakt, och vice versa. Ett företag vars efterfrågeelasticitet är hög (flack efterfrågekurva) har en liten marknadsmakt. Ett företag var efterfrågeelasticitet är låg (brant efterfrågekurva) har en stor marknadsmakt Vid perfekt konkurrens har företagen ingen marknadsmakt, eftersom elasticiteten för dessa är extremt hög. Horisontell MC och MR(?) Exempel: Vi har följande efterfrågefunktion, kvantitet och pris: P = 24 - Q Q = 24 - P dQ/dP = -1 QM = 6 PM = 18 Vi kan räkna ut elasticiteten: ε = dQ/dP * P/Q ε = -1 * 18/16 ε = -3 Lerner-index (L): L = -1/ε L = -1/-3 L = 0.33 Detta ger oss ett mått på företagets marknadsmakt. Vi kan därigenom räkna ut marginalkostnaderna (MC): (P - MC) / P = 0.33 (18 - MC) / 18 = 0.33 18 - MC = 0.33 * 18 -MC = 0.33 * 18 - 18 MC = 18-0.33 * 18 MC = 12 Naturligt monopolNaturligt monopol dvs ett monopol vars genomsnittskostnader avtar för hela marknadens efterfråga. AC = C(Q)/Q För att kunna få ner produktionskostnaderna till de lägsta nivåerna krävs att endast ett företag producerar, eftersom genomsnittskostnaderna är konstant avtagande. Men utan regleringar vet vi också att monopolet kommer ta ut överpriser. Exempel: Telecom-utbyggnaden i Sverige. Inget företag hade ett utbyggt system, så flera företag kunde ta delar av den. Ogliopol. Men elnätsbranschen annorlunda. Mycket svårt för nya företag att ta sig in på marknaden. Stora etableringshinder, skulle kräva att företaget är nästa lika stort som de etablerade, vilket är nästan omöjligt. SRAC (Short-run average costs) Egentligen brukar man rita upp MC som horisontell. Överpris vid P1. För att motverka detta krävs reglering. T.ex prisreglering: AC-prissättning - Genomsnittskostnadsprissättning. där AC skär efterfrågan. Här är intäkterna man får exakt lika stor som kostnaden per enhet. Detta ger noll vinst, dvs π = 0 MC-prissättning - Marginalkostnadsprissättning. där MC skär efterfrågan. Här får vi den kvantitet vi skulle önska vid marknadsjämvikt, om man ser MC som utbudskurvan (utbudskurvan utgör alla företags samlade MC på marknaden). Företaget gör förlust, π < 0. Därför krävs subvention med hjälp av skattemedel. Vi skulle ta in skatt från en verksamhet som vi värderar lägre för att subventionera denna. Subvention per enhet = AC - priset när MC skär efterfrågan. Arean vi får om vi multiplicerar subventionen per enhet gånger Q vid detta pris ger oss de totala kostnaderna för subventionen. Perfekt konkurrens - enskilt företag: Monopol - enskilt företag: Horisontell MC. |
Fortsättningskurs >